机器学习实战-7AdaBoost提升算法

发表于 | 分类于 | 次阅读
字数统计: 2.9k | 阅读时长 ≈ 11

这一章的主要思想就是“三个臭皮匠赛一个诸葛亮”。一般而言，我们都是通过一个分类器进行分类，但是一个分类器可能会出现偶然误差错误，就像一个人总会出现失误一样。所以，我们学习多个不同的分类器，然后将这些分类器通过加上不同的权重组合起来，就形成了一种强大的集成分类器。而这其中，可以再次改进，对不同的分类器，分类效果不同的，权重也可能不同，这样，分类效果好的分类器能够得到更大的“投票权”

前言

  • 元算法/集成学习：即考虑多个专家的意见而不是一个人独断专权
  • AdaBoost：
    • 优点：泛化错误率低，易编码，无参数调整，可使用在大多数分类器上
    • 缺点：对离群点敏感，即对极端值拟合不好（如极大极小值）

7.1 数据如何划分–多重抽样分类器（集成学习的分类）

  • 7.1.1 bagging：Bootstrap aggregating，引导聚集算法/装袋算法
    • 原理：从原始数据总随机有放回的抽取n次组成一个数据集，训练为一个分类器。这样重复进行m次,就得出m个分类器。分类器的权重相等。记住这些分类器数据集是并行进行的，与boosting有区别。
    • 改进算法：随机森林（random forest）
  • 7.1.2 boosting（Boost–增强）
    • 原理：与bagging类似，不同的是，每个分类器的数据集不是并行的，而是串行的。即每个新的分类器都是根据已经训练出来的分类器的性能来进行训练的，之后的分类器需要使用到之前已经训练好的分类器的数据集。boosting集中关注那些被错误分类的数据集。
    • bagging分类器的权重是相等的，boosting的权重是不相等的，每个权重代表的是分类器在上一次迭代时的成功度。
    • boosting的版本有很多，AdaBoost是其中一种（AdaBoost–Adaptive Boosting–自适应增强）

7.2 原理和算法

  • 这里含有许多的公式证明，即为什么使用这些公式，而不使用其它的公式，其中的道理，很难说的清除，暂且保留（可参考《统计学习方法》P139，《西瓜书》P175）
  • 第一个分类器的权重alpha:
    • 定义错误率w = (被错误分类的样本)/(样本总数)
    • alpha = （1/2）*ln((1-w)/w);即错误率越低，权重越大。实际代码操作，变化巨大
  • 一个分类器中每个样本的权重更新：
    • D = D * exp(+-1 * alpha) / sum(D);被正确分类则为-1，否则为+1。注意：这里在代码中有技巧，因为标签为+-1，可以抵消

7.3 单层决策树–决策树桩（decision stump）

  • 代码boost.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
""" 
@author: zoutai
@file: boost.py
@date: 2017/11/04
@description: 单层决策树-找出最好的一个特征，且最好的中间阈值;
"""
from numpy import *
from unit07.adaboost import *

# 这个函数的作用是：对第dimen个特征进行分类，样本点dimen特征小于阈值的被标记为-1，否则标记为+1,。
# 输出为M*1的二维数组，相当于把每个样本当做只有一个特征来划分。这里的1、-1对应标签的1、-1，后面会比较。
# 注意：这里需要对python特别熟悉，shape(dataMat)[0] == m；
# dataMat[:,dimen] <= threshVal返回的是第一列下标，逻辑复杂但是表达却相当简化，这也许就是python的魅力吧
def stumpClassify(dataMat,dimen,threshVal,threshInequal):
    sampleArray = ones((shape(dataMat)[0],1))
    if threshInequal == 'lt':
        sampleArray[dataMat[:,dimen] <= threshVal] = -1.0
    else:
        sampleArray[dataMat[:,dimen] > threshVal] = 1.0
    return sampleArray

def buildStump(dataArr, classLabels,D):
    dataMat = mat(dataArr);labelMat = mat(classLabels).T
    m,n = shape(dataMat)
    numSteps = 10;
    bestStump = {}; # 用于保存重要的结果值，如阈值，样本中节点下标等。
    bestClass = mat(zeros((m,1))) # 分类结果mat，与sampleArray对应
    minError = inf
    # 遍历特征变量
    for i in range(n):
        # 找出第i个特征值的最小值和最大值
        rangeMin = dataMat[:,i].min();rangeMax = dataMat[:,i].max()
        stepSize = (rangeMax-rangeMin)/numSteps # 每一步特征值间隔

        for j in range(-1,int(numSteps)+1):
            for inequal in ['lt','gt']:
                threshVal = (rangeMin+float(j)*stepSize)
                dimenPredictedVals = stumpClassify(dataMat,i,threshVal,inequal)
                errArr = mat(ones((m,1)))
                errArr[dimenPredictedVals == labelMat] = 0 # 正确分类的设为0，错误的默认为1
                # 重点来了，这里才是提升树的核心：通过D来调整特征值对应权值w的比重。D第一次需要初始化
                weightError = D.T*errArr
                print("split: dim %d,thresh %.2f,hresh inequal: %s,the weighted error is %.3f" % (i,threshVal,inequal,weightError))

                if weightError < minError:
                    minError = weightError
                    bestClass = dimenPredictedVals.copy() # 会被修改，所以需要copy
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump,minError,bestClass
  • 代码adaboost.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110

from numpy import *
from unit07.boost import *

""" 
@author: zoutai
@file: adaboost.py 
@date: 2017/11/04
@description:
"""

def loadSimpData():
    datMat = matrix([[ 1. ,  2.1],
        [ 2. ,  1.1],
        [ 1.3,  1. ],
        [ 1. ,  1. ],
        [ 2. ,  1. ]])
    classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
    return datMat,classLabels

def adaboostTrainDS(dataArr,classLabels,numIt):
    weakClassArr = [] # 弱分类器
    m = shape(dataArr)[0]
    D = mat(ones((m,1))/m)
    sumBestClass = mat(zeros((m,1)))
    for i in range(numIt):
        bestStump,error,bestClass = buildStump(dataArr,classLabels,D)
        print(D.T)
        # 核心：alpha是单个分类器的权重
        alpha = float(0.5*log((1.0-error)/max(error,1e-16))) # 这里max是防止分母为0
        bestStump['alpha'] = alpha
        weakClassArr.append(bestStump)
        print(bestClass.T)
        # 更新每个决策树的权重
        # 以下使用了P117和P118的公式
        expon = multiply(-1.0*alpha*mat(classLabels).T,bestClass) # classLabels*bestClass 相同则为正
        D = multiply(D,exp(expon))
        print("---",sum(D))
        D = D/D.sum()

        # 以下是为了累计计算错误率，当错误率为0时，终止循环。
        # 但是我有个疑问，问什么要乘以alpha？。如果不乘以alpha，后面也不用sign函数，不可以吗？
        sumBestClass += alpha*bestClass
        print(sumBestClass.T)
        sumError = multiply(sign(sumBestClass) != mat(classLabels).T,ones((m,1)))
        errorRate = sum(sumError) / m
        print("total errorRate is : ",errorRate)
        if errorRate == 0.0:
            break
    return weakClassArr,sumBestClass

# 对给定数据，在每一个分类器上都进行分类，然后加权求解
def adaClassify(testData,classArr):
    testMat = mat(testData)
    m = shape(testData)[0]
    sumClassArr = mat(zeros((m,1)))
    for i in range(len(classArr)):
        oneClassArr = stumpClassify(testMat,classArr[i]['dim'],classArr[i]['thresh'],classArr[i]['ineq'])
        sumClassArr += classArr[i]['alpha']*oneClassArr
        print(sumClassArr) # 加权计算每一个分类，
    return sign(sumClassArr)


# 将文本数据转化为矩阵训练数据
def loadDataSet(filename):
    dataMat = []; labelMat = []
    file = open(filename)
    for line in file.readlines():
        lineArr = []
        line = line.strip().split()
        for i in range(len(line)-1):
            lineArr.append(float(line[i]))
        dataMat.append(lineArr)
        labelMat.append(float(line[-1]))
    return dataMat,labelMat

# ROC曲线绘制及AUC计算函数
def plotROC(sumClass,classLabels):
    import matplotlib.pyplot as plt
    cur = (1.0,1.0)
    ySum = 0.0
    numPosClas = sum(array(classLabels) == 1.0) # 计算真阳例的分母--真实结果为正的数目
    numNoPosClas = len(classLabels) - numPosClas # 计算假阳例的分母--...
    yStep = 1/float(numPosClas) # y轴上个步进长度，下同理
    xStep = 1/float(numNoPosClas)
    sortedIndicies = argsort(sumClass) # 重点：argsort函数返回的是数组值从小到大的索引值 参考：http://blog.csdn.net/maoersong/article/details/21875705
    fig = plt.figure()
    fig.clf()
    ax = plt.subplot(111)
    # 这里理解是一个难点！
    # 1、书上说了，由于排序是由大到小，也就是，开始值小的部分，训练师被分为-1，之后数大的部分被分为+1；所以只能从右上开始画。、
    # 这样，显然开始画图部分是从不预测值不是+1开始的
    # 但是看图时，是从左下开始，预测值更可能是1.0
    # 表达能力有限啊!我自己都说不清楚。。
    # 这个ROC开起来可能好像没用到训练情况，其实，这里的关键在于排序。这样，排序的前面所有都是-1，后面所有都是+1；。
    # 但是为什么没有使用预测结果，因为最终都将是归为x=1,y=1.目的是让+1尽可能靠近前面，面积AUC更大，这就是ROC的意义！
    for index in sortedIndicies.tolist()[0]:
        if classLabels[index] == 1.0: # 这里的1.0是指预测为正，将实际值classLabels与此比较，如果相同，y值下降
            delX = 0;delY = yStep;
        else:
            delX = xStep;delY = 0;
            ySum += cur[1]
        ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY],c='b')
        cur = (cur[0]-delX,cur[1]-delY)
    ax.plot([0,1],[0,1],'b--')
    plt.xlabel('False positive Rate');
    plt.ylabel('True positive Rate');
    ax.axis([0,1,0,1])
    plt.show()
    print("the Area Under the Curve is :",ySum*xStep)
  • 测试代码test.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
""" 
@author: zoutai
@file: test.py 
@time: 2017/11/04 
@description: 
"""

# 这里记录一个python错误：当两个类出现互相调用时，可能会出现无法调用的情况，如adaboost和boost两个方法互相调用
# 所以，测试运行代码尽量另外单独写，比如test
from unit07.adaboost import *

# # 测试1:基于加权的分类器
# dataMat,lebalMat = loadSimpData()
# # D是这里的核心：D是每一个样本的权重，通过D.T*errArr来得出错误率，除以m是为了归一化
# # 在单层决策树中并没有迭代，但是才后面的提升过程中，主要就是D的不断迭代修改，来进行训练优化
# D = mat(ones((5,1))/5)
# bestStump,minError,bestClass = buildStump(dataMat,lebalMat,D)
# print(bestStump)
# print(minError)
# print(bestClass)

# # 测试2:基于adaboost的弱分类器，多个阈值，单层
# dataMat,lebalMat = loadSimpData()
# weakClassArray = adaboostTrainDS(dataMat,lebalMat,9)
# print(weakClassArray)

# # 测试3：测试一个数据集，看效果
# dataMat,lebalMat = loadSimpData()
# # 这里的30是迭代次数，也是分类器个数。其实3次时，errorRate==0,就够了，此时分类器就是3个
# weakClassArray = adaboostTrainDS(dataMat,lebalMat,30)
# predictResult = adaClassify([[0,0]],weakClassArray) # [[0,0]]这个地方书上写错了
# print("the result is:",predictResult)

# # 测试4-马疝病-预测得病的马是否能存活
# dataMat,lebalMat = loadDataSet('horseColicTraining2.txt')
# classArr = adaboostTrainDS(dataMat,lebalMat,10)
# print(classArr)
# testMat,testLabelMat = loadDataSet('horseColicTest2.txt')
# predictArr10 = adaClassify(testMat,classArr)
# num = len(testMat)
# errorArr = mat(ones((num,1)))
# errorRate = sum(errorArr[predictArr10 != mat(testLabelMat).T])/num
# print(errorRate)
# # 说明一点，这里的数据与第四章不同；另外我的测试结果和书上也不同
# # 测试结果：
# # 1   --   0.367892976589   --   0.283582089552
# # 10  --   0.354515050167   --   0.328358208955


# 画ROC曲线
# 疑问：这个地方实在是没弄懂，这个曲线有什么用？只是用了训练的排序，没有用训练的预测值。
dataMat,lebalMat = loadDataSet('horseColicTraining2.txt')
classArr,sumClass = adaboostTrainDS(dataMat,lebalMat,10)
plotROC(sumClass.T,lebalMat)

后续：

  1. 非均衡分类器

    –| 即训练出来的分类器并不是一定准确的，即便错误率很低，但是在某些情况下在这种错误是不能出现的。比如，垃圾邮件的分类，本来是好的邮件被当做垃圾邮件会造成邮件的丢失。
    –| 一般而言，这种分类器是由于正例样本和反例样本数目相差很大造成的。

  • 分类的其他度量指标：正确率、召回率、ROC曲线
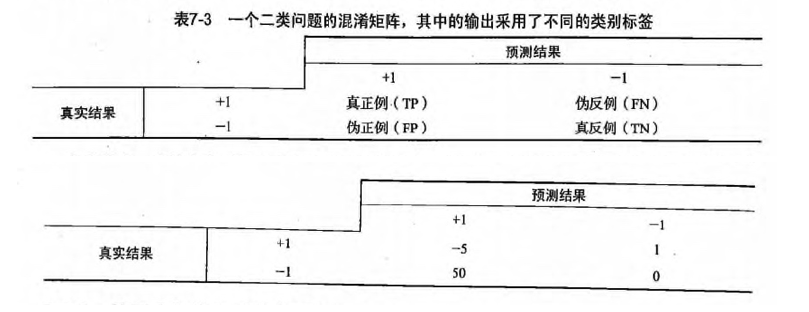
    • 1正确率：前面使用的就是正确率来度量，但是我们可以改进前面的度量方式。如采用混淆矩阵（书中后面讲到的代价函数)
    • 2召回率：预测为正的数据占所有实际为正例的比例。在召回率很大时，真正判错的正例不多
    • 3ROC曲线，当面积AUC越大，说明分类器越好，作为模型选择的一种方式
      混淆矩阵
  1. 处理分均衡问题的数据抽样方法

    即对某一个类别的样本少的进行重复抽样–过抽样；对样本多的进行少抽样或删除–欠抽样

总结：集成分类器可能进一步突出单个分类器的不足，如过拟合问题；但是如果分类器之间的差别较大时，这个问题就会缓和一些。这种不同可以使算法不同，也可以是数据不同。

Donate comment here