最近正在做一个语音分离的任务,其中有一个语音分离的方法叫做NMF,中文非负矩阵分解,即将矩阵表示为V=WH,mn = mr * r*n;其实这种矩阵分解的方式和本章的内容类似,也是对矩阵进行降维或者简化矩阵;其实有时候并不仅仅是降维,这种方式,也是一种变相提取特征值得过程,其中的W相当于特征向量组,H相当于特征的权重向量组。即PCA不仅仅对数据进行降维,降低了数据的运算量;同时也是一种提取特真的好方法。
一、前言
什么是降维,想象一下,初中时我们学习物理,记得老师经常说,让我们把一个物体看做一个“质点”,比如足球,它就是一个点,就不要关注上面的花纹。所以在足球比赛时,尽管电视机的画面很多,有花有草还有“演员”,但是我们关注的只是足球那一个点。这里的思想其实就是降维,即去掉我们不需要关注的数据或者维度
二、降维技术
几种降维技术:
- 主成分分析PCA(principal component analysis):将数据从原始的坐标系转换到新的坐标系。第一个坐标系选择为原数据方差最大的方向(最大吗?我咋感觉是最小。。),第二个坐标系选择与第一个坐标系(上一个)相正交且方差最大的方向,以此类推,重复次数为原始数据的维数。其实,最后我们发现,大部分方差都包含在前面的几个坐标轴中,所以只需要取前几个坐标轴就行,这就降维了!举个例子:就相当于,我们分类人群性别时,如果知道人群的头发是否是长头发和是否穿牛仔,牛仔的辨识度很差,基本可以抛弃,就不用在考虑这个特征(男女都穿牛仔,没有区分度)
- 因此分析FA(factor analysis):这个有点像我们线性倒数中的求解矩阵的基,或者说是单位向量。我们的数据很多,但是猜测我们的数据都是有某些单位向量(隐变量)线性组合来的。即,给了很多坐标数据(1,1)(2,2)(1,3)(2,6)(3,9),看起来很复杂,仔细想想,其实只需要两个数据就能表达,即(1,1)和(1,3),其他都是这两个点的线性组合。官方定义:假设观察数据是某些隐变量和某些噪声的线性组合,我们只需要找到这些隐变量就行
- 独立成分分析ICA(independence component analysis):这个和FA有点类似,应该就是单通道语音分离的方式。但是与FA不同的是,我们的这些基(隐变量)不是单个的,可能是一个组合或者一个高斯模型。即我们假设我们的数据是由N个互相独立的数据源组成,与PCA不同,这些数据源互相独立就,这样我们就能分别分离。比如,一个混合的语音信号,这里面有张三的话、李四的话和王健林的话,这里面张三这几个人的话就是相互独立的数据集。
三、PCA
转载:
优点:降低数据的复杂性,识别最重要的多个特征。
缺点:不一定需要,且可能损失有用信息。
使用数据类型:数值型数据。
- 移动坐标轴
考虑一下图1中的大量数据点。若要求画出一条直线,这条线要尽可能覆盖这些点,三条直线中B最长。在PCA中,对数据的坐标进行旋转,该旋转的过程取决于数据的本身。第一条坐标轴旋转到覆盖数据的最大方差为止,即直线B。数据的最大方差给出了数据的最重要的信息。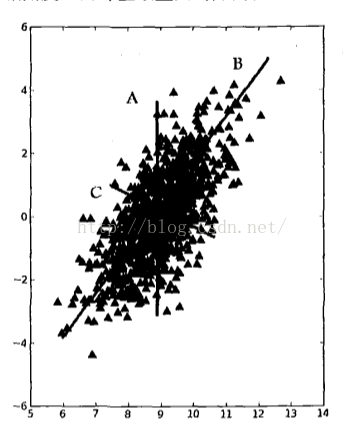
在选择了覆盖数据最大差异性的坐标轴后,继续选择第二条坐标轴。假如该坐标轴与第一条坐标轴垂直,它就是覆盖数据次大差异性的坐标轴。更严谨的说法是正交(orthogonal)。在二维平面下,垂直和正交是一回事。在图1中,直线C就是第二条坐标轴。利用PCA,可将数据坐标轴旋转至数据角度上的那些最重要的方向。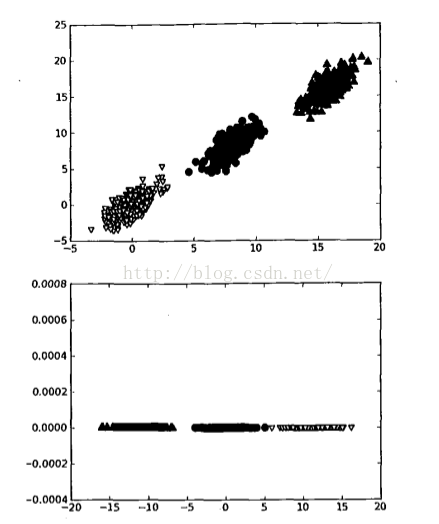
实现坐标轴旋转后,可讨论降维。坐标轴的旋转并没有减少数据的维度。图2中包含三个不同的类别。要区分这三个类别,可使用决策树。决策树每次都是基于一个特征来做决策。我们会发现,在x轴上可找到一些值,这些值能够很好地将这3个类别分开。这样可得到一些规则,比如当(X<4)时,数据属于类别0。若使用SVM这样稍复杂的分类器,可得到更好的分类面和分类规则,比如当(w0x + w1y + b) > 0时,数据也属于类别0。SVM可能比决策树得到更好的分类间隔,但分类超平面却很难解释。
通过PCA进行降维处理,可同时获得SVM和决策树的优点:一方面,得到了和决策树一样的简单分类器,同时分类间隔和SVM一样好。考虑图2中下面的图,其中的数据来自于上面的图并经PCA转换后绘制而成。如果仅使用原始数据,那么这里的间隔会比决策树的间隔大。另外,由于只需要考虑一维信息,因此数据可通过比SVM简单得多的、且容易采用的规则进行区分。
在图2中,只需一维信息即可,因为另一维信息只是对分类缺乏贡献的噪声数据。在二维平面下,这看上去微不足道,但在高维空间则意义重大。
对PCA的基本过程简单阐述后,接下来可通过代码实现PCA过程。前面提到第一个主成分就是从数据差异性最大(即方差最大)的方向提取出来的,第二个主成分则来自于数据差异次大的方向,并且该方向与第一个主成分方向正交。通过数据集的协方差矩阵及其特征值分析,可以求得这些主成分的值。
一旦得到了协方差矩阵的特征向量,就可以保留最大的N个值。这些特征向量也给出了N个最重要的真实结构。可以通过将数据乘上这N个特征向量而将它转到新的空间。
- numpy实现PCA降维
代码:pca.py
1 | """ |
代码:test.py
1 | """ |
小结
本章的PCA降维要求将所有的数据都调入内存,即离线形式;目前有一种在线方式的PCA分析,可以参考论文:Incremental Eigenanalysis For Classification
参考链接:http://blog.csdn.net/zhongkelee/article/details/44064401

