虽然本章标题是SVD,但是感觉本章的内容核心却有点像是推荐系统,SVD的主要作用优化数据,简化运算。对于推荐系统,生活中处处都是,比如火热的网易云音乐,其中就是用到的因子推荐算法,记得我的第一篇博客就是从知乎上转载下来的;另外还有今日头条;其他的应用其实也有,但是自我感觉,这两个应用应该是最好的。记得最近俱乐部有一个网络订餐推荐系统的项目,而这正是书中所举的例子,作为一个推荐系统,其实饮食推荐系统和音乐推荐有很多类似或者可能完全相同处理。它的基本逻辑就是找和你经常吃同样美食的用户A,然后给你推荐用户A吃过的,而你却没吃的。比如你和A,你们都喜欢吃川菜,但是A吃过夫妻肺片,并且对其评价很好,而你没吃过,这时候,推荐系统通过计算就很可能给你推荐夫妻肺片。
由于吴军《数学之美》中对此解释非常好,所以这里转载:
“三个矩阵有非常清楚的物理含义。第一个矩阵X中的每一行表示意思相关的一类词,其中的每个非零元素表示这类词中每个词的重要性(或者说相关性),数值越大越相关。最后一个矩阵Y中的每一列表示同一主题一类文章,其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章雷之间的相关性。因此,我们只要对关联矩阵A进行一次奇异值分解,w 我们就可以同时完成了近义词分类和文章的分类。(同时得到每类文章和每类词的相关性)。”
一、SVD的应用
优点:简化数据、去除噪声、提高算法效果
缺点:逻辑转换可能难以理解
使用类型:数值型数据
- 隐性语义索引LSI(信息检索)
这里,我谈谈我的理解,可能不太准确。首先我们谈谈一般搜索的两个问题:
- 关键词写错。比如我搜索“北晶”,我的本意是搜索“北京”,但是搜索引擎还是会给我推荐“北京”的结果。为什么?如果是简单的搜索,搜索引擎将查找所有与“北晶”相关的信息,而忽视“北京”。但是通过SVD,可以将“北京”“背景”“背静”等相似拼音的词语归为一个集合,这样,当搜索不存在是就会判断是否输入错误,已在集合里面查找相关的词语。
- 同义词搜索。比如我们搜索“SVD”,尽管SVD和PCA可能存在许多的差别,但是在系统内部,由于使用SVD对所有的文章进行处理后发现,SVD和PCA经常一起出现在一篇文章中,因此将这两个次聚为一类,这时当我们搜索“SVD”时,其实,也会给我门提供PCA的信息。
上面就是SVD对搜索引擎的改进
- 推荐系统
在前言中,通过餐厅个性化订餐系统讲述了SVD的应用,其实,这是和信息检索一个道理,就是找到和你口味相同的所有用户,推荐他们吃过,而你没吃过的食物。
二、矩阵分解和推导
SVD也是对矩阵进行分解,但是和特征分解不同,SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵,那么我们定义矩阵A的SVD为: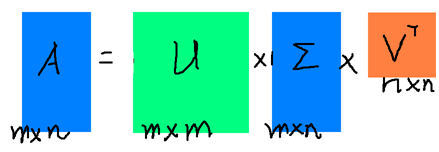
其中U是一个m×m的矩阵,Σ是一个m×n的矩阵,除了主对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值,V是一个n×n的矩阵。U和V都是酉矩阵,即满足UTU=I,VTV=I。下图可以很形象的看出上面SVD的定义: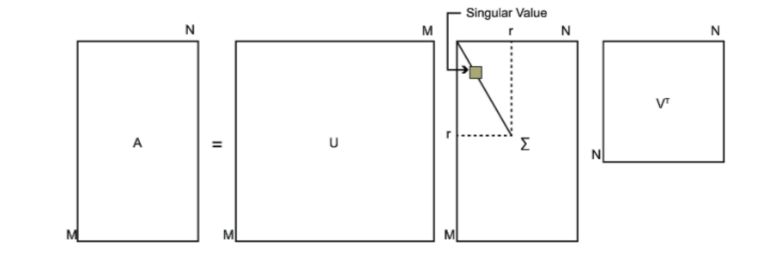
具体的数学逻辑推导参考:知乎
三、SVD实际应用案例
接下来是通过SVD来优化推荐系统,以及压缩图像
首先梳理几个点:
- 1.原始推荐系统如何推荐:一般推家系统都是通过计算两个用户的相似度,来进行更推荐
- 2.相似度的计算:(最后都要归一化到0-1)
- 欧式距离
- 余弦相似度
- 皮尔逊相关系数

- 3.改进推荐系统:原始的推荐系统需要大量的计算,通过使用SVD简化数据,能够大大加快运算的速度
- 4.重构矩阵:即尽可能的保留原始矩阵的信息
- 我们可以发现得到的特征值,前3个比其他的值大很多,所以可以将最后2个值去掉,因为他们的影响很小。
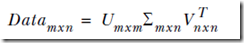
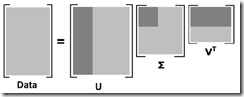
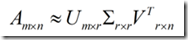
- 上面例子就可以将原始数据用如下结果近似:
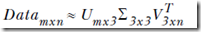
- 我们可以发现得到的特征值,前3个比其他的值大很多,所以可以将最后2个值去掉,因为他们的影响很小。
四、推荐系统和图像压缩案例1、2
- 代码svdRec.py
1 | """ |
- 测试代码:test.py
1 | """ |
最后、补充内容
- 推荐引擎的检验:检查检验、最小均方根误差
- 推荐系统其他的改进
- 大规模数据,SVD会降低程序的速度,SVD可以在调入时运行一次。之后每天运行一次或者频率更低。不需要频繁运行。并且需要离线运行
- 节约存储空间:通过观察,我们发现,上面的矩阵存在很多的0值,所以可以不保存这些值,节约内存和计算开销
- 另外相似度得分不需要每次都计算:可以离线保存相似度得分。另外计算时,物品之间的相似度不同的用户是一样的可以复用
- 冷启动(面试):即对于一个新用户或者新的商品,如何推荐?没有相关数据
- 可以首次推荐当做搜索问题来处理,用户主动搜索才会出现
- 对于图像压缩:如果理解SVD的数学公式推导,就不难理解,其实,就是将像素在坐标轴上进行压缩。比如高中,我们学数学向量坐标时,经常做的作业就是平移压缩扩大,比函数y=f(x),横坐标缩小两倍就是:y=f(2x)

