机器学习实战-8预测数值型数据-回归

发表于 | 分类于 | 次阅读
字数统计: 2.8k | 阅读时长 ≈ 12

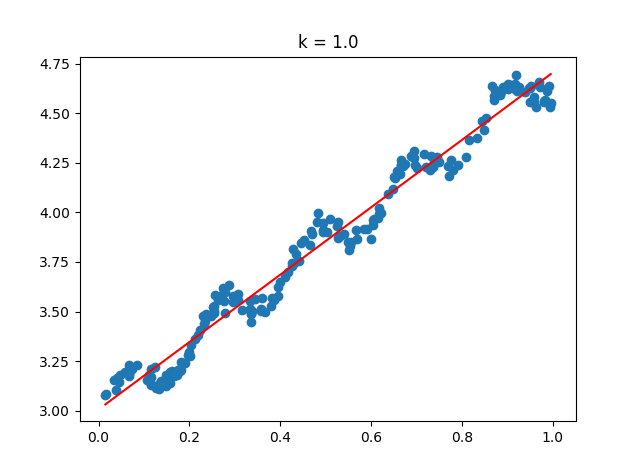
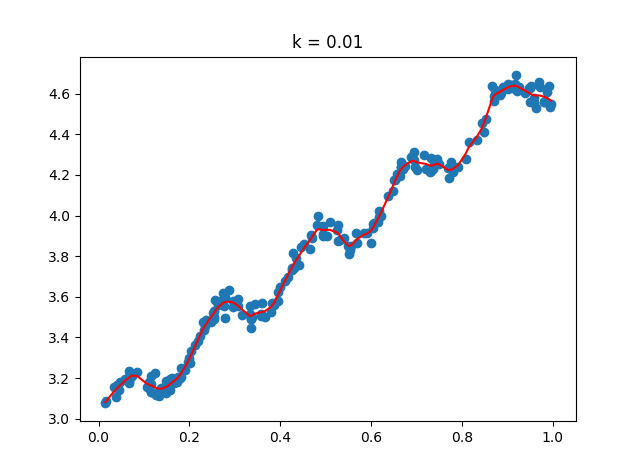
回归和分类是机器学习两个主要的类别，通常会在面试的时候，被询问这两者之间的区别。对于我，有时候我也无法说清，虽然我感觉我已经弄懂了，但是这里还是说一说自己的理解。首先，我们学过一本书《随机过程》，这里面讲到了马尔科夫链等，这是一种在时间、位置等有序列属性的数据，也就是说，这些说句不仅仅存在关系，而且存在一种序列上的前后关系，如时间、地理位置等。而分类一般核心不在于此。所以，回归问题就是一种序列预测问题，比如预测房价-时间、房间-面积、股票-时间等序列关系，通过模拟之前的序列来预测之后的序列。最简单，如线性回归，这就像我们解一元方程y=ax一样，解出a就可以了。但是，存在一个问题，这个直线是不是太直了，可能是个曲线了？或者说，更应该是是一个近似曲线的波浪线了？所以，回归的问题就开始复杂了，此时，我们开始了一些波动预测。采用的一种方式就是，对于每一个数据都有一个权重，而不是只有一个。即我们不是求单个方程，而是求解整个片段的方程，每一个点都有权值，遮掩，我们就将这个权值序列向后移动，以此来预测后来的值，即已有[1-100],那么就可以预测[2-101]来得出x=101的值，以此类推。

一、线性回归

通俗一定，线性回归就是多元以此方程组，多元指的就是多个特征值。回归最早是由达尔文的表兄弟发明的，当时他的目的是为了通过豌豆上一代的尺寸来预测下一代的尺寸，这正是回归问题。为什么叫做回归？是因为当时他发现一般人的身高虽然遗传来自父母，但是整体上还是会向均值靠近，即回归（即便他的父母很高），这个名词和这里的意义不大，但是还是有那么点意思，即任何数据都会靠近正常预测水平，不会太不靠谱（强行解释–）

  1. 原理
    一般使用平方误差计算（因为单减误差会互相抵消）：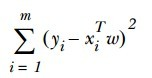
    enter description here
    对w求导，等于0，得：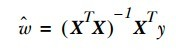
    enter description here
  1. 衡量分离的好坏，有一个方式就是通过corrcoef函数来求解相关系数，越接近0，相关性越大，说明预测越好

enter description here

二、局部加权回归

线性回归有个很大的缺点，即欠拟合，太直了，不知道转弯，就是一条直线（它求得是最小均方误差的无偏估计）；所以，为了防止这种情况，引入一些偏差进来，相当于做一个缓冲作用，从而降低均方误差。局部加权回归LWLR就是其中的一种

  1. 对每一个数据都加入一个权重系数W,最终的回归系数w就是：
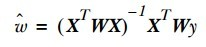
    enter description here
  2. 核
    这里的核类似于支持向量机中的核，通过这个核来对附近的点赋予更高的权重，一般使用的是高斯核：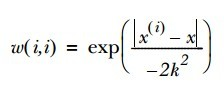
    enter description here
  3. 注意，这里的代码和线性回归不同，因为它不是一条直线，而是每个点都是一个单独计算的，所以最后的划线是片段性的。

enter description here

**三、缩减系数来“理解”数据

对于分类还是回归问题，我们时常遇到数据特征比样本数量还多的情况。如果是这种情况，由于(xTx)^-1不能计算，所以是无法解决的。为了解决这个问题，我们想到了在矩阵中加入一个额外的数据，类似于补充特征。这里讲述两种方式：岭回归和lasso法(本文采用类的前向逐步回归)

  1. 岭回归
  • 岭回归就是在上面提到的矩阵上加一个λI 从而使矩阵非奇异（参考奇异值分解），这样就可以求逆了。之后的公式为：
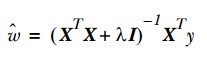
    enter description here
  • 为什么叫做缩减？因为通过引入惩罚项后，可以限制所有w的和，这样就能够减少不重要的参数，在统计学上就叫做缩减，这样能更好的理解数据（奇异值分解就是这个作用，提取出关键的信息点）
  • 标准化问题：这里对特征进行了标准化处理，以使特征具有相同的重要性（这里的处理类似于归一化，但是在归一化的基础上又除以了跨度值）；而对于结果y只有归一化。
    enter description here
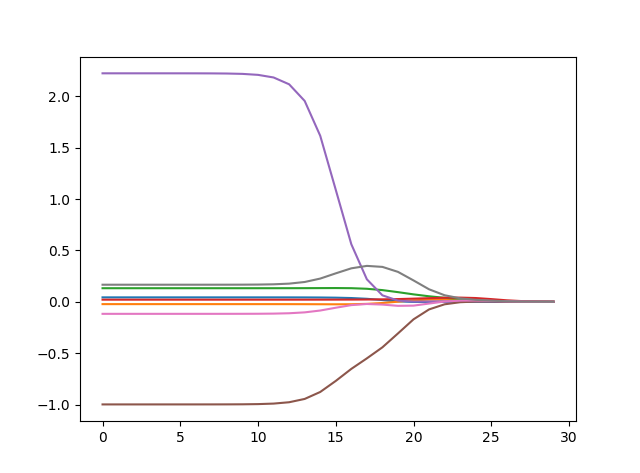
  1. lasso
  • 这种方式通过对每一个点进行上下浮动取值，来定点优化；从而遍历优化所有的w
    enter description here
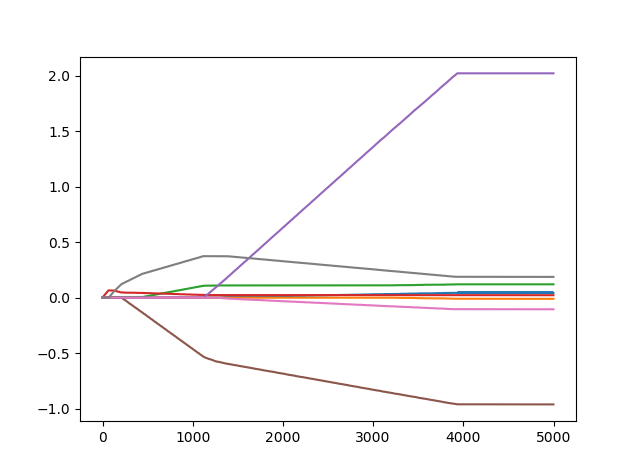
  • 四、代码*
  1. regression.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
""" 
@author: zoutai
@file: regression.py 
@time: 2017/11/24 
@description:逻辑回归
"""

# 相对于分类所不同的是，逻辑回归更适合处理数据之间有连续关系的数据
# 线性回归就像是近似拟合直线，比如房价的走势等，找到一条最近似的直接来进行模拟，以便于能够预测将来的数据


from math import *
from numpy import *

def loadDataSet(fileName):      #general function to parse tab -delimited floats
    numFeat = len(open(fileName).readline().split('\t')) - 1 #get number of fields
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat,labelMat

# 1、线性回归-最小二乘法
# 求解线性回归的权重参数w，求导解，公式为：w=(X.T * X)^(-1) * (X.T * Y)
def standRegres(xArr,yArr):
    xMat = mat(xArr);yMat = mat(yArr).T
    xtx = xMat.T * xMat

    # 这里需要保证xtx的秩不能为0，否则没有逆矩阵-1
    if linalg.det(xtx) == 0.0:
        print("This matrix is single,cannot do inverse")
        return
    w = xtx.I * (xMat.T * yMat)
    return w

# 2、局部加权回归LWLR
# 1中的线性回归有个问题，就是欠拟合，太老实了；不知道转个弯变通一下。因为它求的是最小均方误差的无偏估计（即保证整个过程是条直线，不转弯）
# 因此引入一定的偏差，从而降低预测的均方误差

# 与线性回归有一点差别，这里面主要是引入了回归系数w
# 公式为：w=(X.T * W * X)^(-1) * (X.T * W * Y)
def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    m = shape(xMat)[0]
    weight = mat(eye(m))
    for i in range(m):
        diffI = testPoint - xMat[i,:]
        weight[i,i] = exp(diffI * diffI.T/(-2.0*k**2))

    xtx = xMat.T * weight * xMat
    if linalg.det(xtx) == 0.0:
        print("This matrix is single,cannot do inverse")
        return
    w = xtx.I * (xMat.T * weight * yMat)
    return testPoint * w # 注意矩阵相乘是的前后顺序

def lwlrTest(testArr,xArr,yArr,k=1.0):
    m = shape(testArr)[0]
    yHat  = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

def rssError(yArr,yHatArr):
    return ((yArr - yHatArr)**2).sum()


# 3、岭回归
def ridgeRegres(xMat, yMat, lam=0.2):
    xTx = xMat.T * xMat
    denom = xTx + eye(shape(xMat)[1]) * lam
    if linalg.det(denom) == 0.0:
        print("This matrix is singular, cannot do inverse")
        return
    ws = denom.I * (xMat.T * yMat)
    return ws


def ridgeTest(xArr, yArr):
    xMat = mat(xArr);
    yMat = mat(yArr).T
    yMean = mean(yMat, 0)
    yMat = yMat - yMean  # to eliminate X0 take mean off of Y
    # regularize X's
    xMeans = mean(xMat, 0)  # calc mean then subtract it off
    xVar = var(xMat, 0)  # calc variance of Xi then divide by it
    xMat = (xMat - xMeans) / xVar
    numTestPts = 30
    wMat = zeros((numTestPts, shape(xMat)[1]))
    for i in range(numTestPts):
        ws = ridgeRegres(xMat, yMat, exp(i - 10))
        wMat[i, :] = ws.T
    return wMat


# 直到这里我才理解回归的精髓，即这里面并不是求解一个w值，而是求出一个序列的w序列，
# 然后根据这个序列预测后一个序列的值！

# 前向逐步线性回归（这里面重点是将x,y归一化；其中x是标准化处理，y进行归一化处理，都汇集到0处，
# 这样，x-y系数就为1，近似单位一的正相关）
# 即求解y=x上下浮动近似

# 正则化
def regularize(xMat):#regularize by columns
    inMat = xMat.copy()
    inMeans = mean(inMat,0)   #calc mean then subtract it off
    inVar = var(inMat,0)      #calc variance of Xi then divide by it
    inMat = (inMat - inMeans)/inVar
    return inMat

# 这里我弄不清了：为什么x需要除以一个数，而y不需要？
def stageWise(xArr,yArr,eps=0.01,numIt=100):
    xMat = mat(xArr);yMat = mat(yArr).T
    yMean = mean(yMat)
    yMat = yMat - yMean
    xMat = regularize(xMat)
    m,n = shape(xMat)

    returnMat = zeros((numIt,n))
    ws = zeros((n,1))
    wsTest = ws.copy()
    wsMax = ws.copy()

    for i in range(numIt):
        print(ws.T)
        lowestError = inf
        for j in range(n):
            for signal in [-1,1]:
                wsTest = ws.copy()
                wsTest[j] += eps * signal
                yTest = xMat * wsTest
                rssE = rssError(yTest.A,yMat.A)
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        returnMat[i,:] = ws.T
    return returnMat
  1. 测试段：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
""" 
@author: zoutai
@file: test.py 
@time: 2017/11/24 
@description: 
"""


from unit08.regression import *

xArr,yArr = loadDataSet("ex0.txt")
xMat = mat(xArr)
yMat = mat(yArr)
w = standRegres(xArr,yArr)
yHat = mat(xArr) * w

import matplotlib.pyplot as plt
fig = plt.figure()
ax =fig.add_subplot(111)

# 1、flatten()将数据都表示称一维数据，但是数据格式还是原来的维数
# 2、A[0]，A相当于原矩阵(?)
ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])

# 这里画图没有排序，下一个实验会发现有错误
ax.plot(xMat[:,1].flatten().A[0],yHat)
plt.show()


# 评测预测准确度：相关系数cov：函数corrcoef()
covMat = corrcoef(yMat,yHat.T)
print(covMat)
# the result is:
# [[ 1.          0.98647356]
#  [ 0.98647356  1.        ]]
# 对角表示自己和自己的关联度，为1,；0.98为这两个的关联度，越接近1，表示越好
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
""" 
@author: zoutai
@file: test.py 
@time: 2017/11/24 
@description: 
"""


from unit08.regression import *

xArr,yArr = loadDataSet("ex0.txt")
xMat = mat(xArr)
yMat = mat(yArr)
#yHat = lwlrTest(xArr,xArr,yArr,0.003)
yHat = lwlrTest(xArr,xArr,yArr,0.01)


import matplotlib.pyplot as plt
fig = plt.figure()
ax =fig.add_subplot(111)

# 1、flatten()将数据都表示称一维数据，但是数据格式还是原来的维数
# 2、A[0]，A相当于原矩阵(?)

# 排序
srtInd = xMat[:,1].argsort(0) # 排序后的序号
xSort = xMat[srtInd][:,0,:]

ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])

ax.plot(xSort[:,1].flatten().A[0],yHat[srtInd],color='red',)
ax.set_title("k = 0.01")
plt.show()


# 评测预测准确度：相关系数cov：函数corrcoef()
covMat = corrcoef(yMat,yHat.T)
print(covMat)
# the result is:
# [[ 1.          0.98647356]
#  [ 0.98647356  1.        ]]
# 对角表示自己和自己的关联度，为1,；0.98为这两个的关联度，越接近1，表示越好


# 预测鲍鱼的年龄(前100个预测后100个)

# 1加权回归法
abX,abY = loadDataSet("abalone.txt")
yHat = lwlrTest(abX[100:199],abX[0:99],abY[0:99],10)
error1 = rssError(yHat.T,abY[100:199])
print("the lwlr error is :",error1)

ws = standRegres(abX[0:99],abY[0:99])
yHat2 = abX[100:199] * ws
error2 = rssError(yHat2.T.A,abY[100:199]) # .A运算应该是将mat矩阵转化为array数组
print("stand error is :",error2)

# the result is :
# the lwlr error is : 517.571190538
# stand error is : 518.636315325



# test3、岭回归
ridgeWeights = ridgeTest(abX,abY)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
""" 
@author: zoutai
@file: test.py 
@time: 2017/11/24 
@description: 
"""


from unit08.regression import *

xArr,yArr = loadDataSet("ex0.txt")
xMat = mat(xArr)
yMat = mat(yArr)
import matplotlib.pyplot as plt
fig = plt.figure()
ax =fig.add_subplot(111)
abX,abY = loadDataSet("abalone.txt")

# test3、岭回归
# 这个地方我没有仔细思考，直接摘录来了
ridgeWeights = ridgeTest(abX,abY)
ax.plot(ridgeWeights)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
""" 
@author: zoutai
@file: test.py
@time: 2017/11/24
@description:
"""


from unit08.regression import *

xArr,yArr = loadDataSet("ex0.txt")
xMat = mat(xArr)
yMat = mat(yArr)
import matplotlib.pyplot as plt
fig = plt.figure()
ax =fig.add_subplot(111)
abX,abY = loadDataSet("abalone.txt")

# test3、岭回归
# 这个地方我没有仔细思考，直接摘录来了
ridgeWeights = stageWise(abX,abY,0.001,5000)
ax.plot(ridgeWeights)
plt.show()
Donate comment here