图算法-Prim、Kruskal、Dijkstra、Floyd、Bellman

发表于 | 分类于 | 次阅读
字数统计: 1.5k | 阅读时长 ≈ 6

现实生活中，我们常常遇到一些涉及到图的问题；比如一个视频网站如何分配网络服务器，才能使得资源成本最小化；几个城市之间要修路，如何规划才能使得成本最小。另外现在是五一，有几个城市路线规划，在考虑路费时间等因素条件下，如何规划旅游路线。这些的种种问题，都可以化为图规划问题。前两个即最小生成树问题，后面一个即最短路径问题。

  • 最小生成树
    最小生成树，即对于一个加权图，如何规划路线，使得图中每个节点都能够连通，且权重成本最小（没有环型结构）

典型算法：Prim和Kruskal

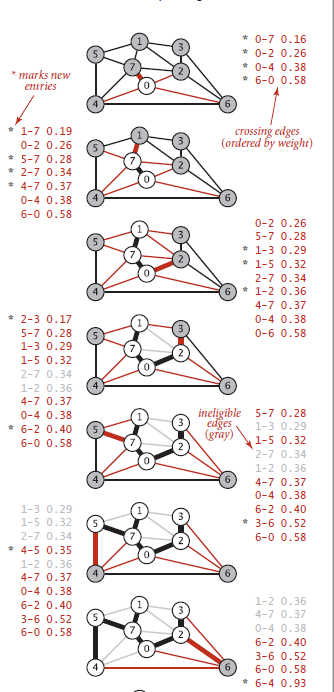
  • Prim算法，请参照《算法4》p399图例

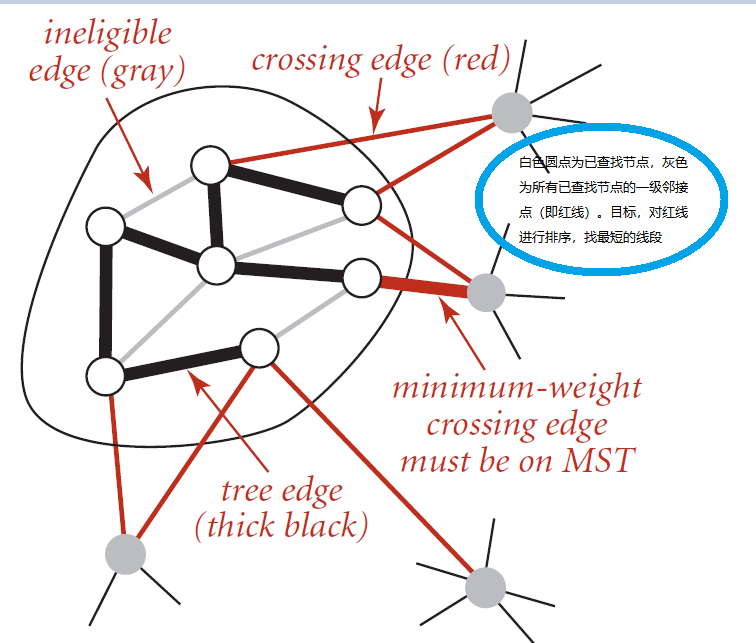
    每次对已访问的节点所连接的外部边进行排序，找到最短的边作为下一个边，进行连接。（重点是已访问）
    prim
    enter description here

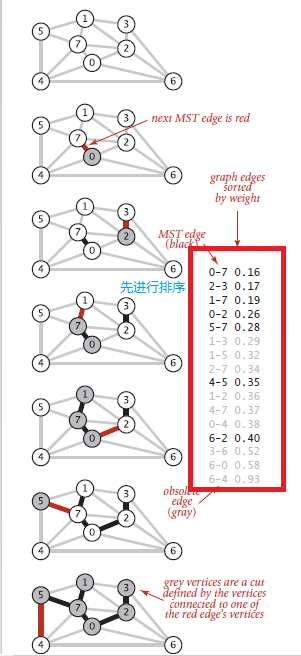
  • Kruskal

    与Prim算法稍微有点区别。Kruskal算法首先将所有的权重边进行排序，然后对排序的遍历连接，直到所有的边都简历连接关系。（所有的边，不仅仅是已访问）
    kuuskal

  • 最短路径问题
    对于一个加权图，对于同种的节点A和B，规划一个路线，使得从A到B的路线最短，有时候，这里的成本还会考虑其他因素，都作为权重计算。

典型算法;BFS,DFS(广度优先搜索和深度优先搜索)；Dijkstra、拓扑排序、bellman、floyd、A*算法

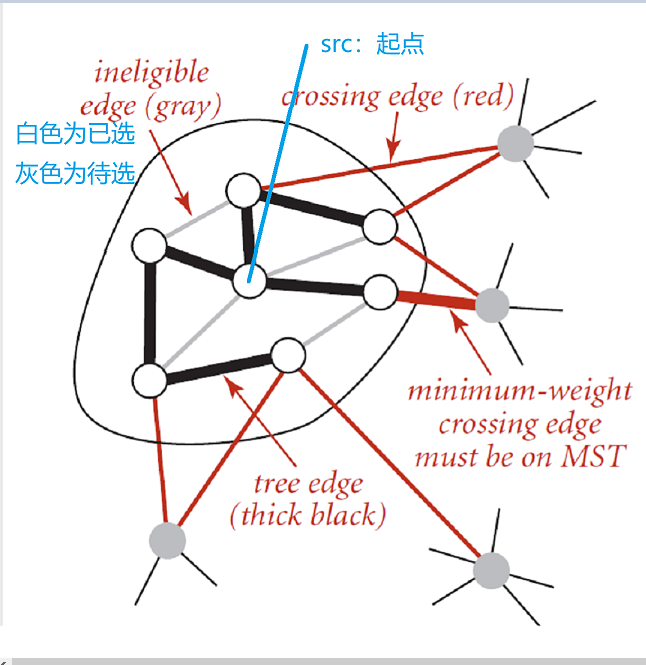
  • Dijkstra

    Dijkstra思想类似于A*算法：graph[src][d]=graph[src][v] + graph[v][d]；其中src为起点，V为已访问节点，d为待访问节点（即相邻的节点）
    Dijkstra

  • Floyd

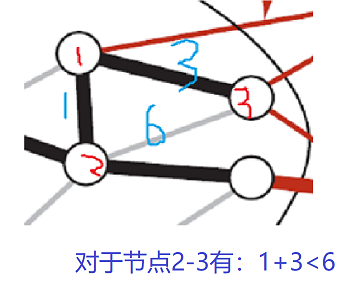
    Floyd思想类似化学催化剂原理，即Dis(i,k) + Dis(k,j) < Dis(i,j)；A直接生成C成本需要100分钟，但是A生成B再生成C总成本：A到B加上B到C可能只有10+20=30分钟，所以，三次遍历整个路径，将所以可以使用催化剂缩短的路径更改，并保存最短路径队列
    Floyd

  • Ford

    Bellman-Ford算法可以非常好的解决带有负权的最短路径问题，什么是负权？如果两个顶点之间的距离为正数，那这个距离成为正权。反之，如果一个顶点到一个顶点的距离为负数，那这个距离就称为负权。Bellman-Ford和Dijkstra 相似，都是采用‘松弛’的方法来寻找最短的距离(为细看，解析保留)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
def prim(graph, root):
    assert type(graph) == dict
    # 待访问节点
    nodes = list(graph.keys())
    nodes.remove(root)
    # 已访问节点
    visited = [root]
    path = []
    next = None
    while nodes:
        # 找出最小距离
        distance = float('inf')
        for s in visited:
            for d in graph[s]:
                # 如果节点已经被访问或者是自身节点，则跳过，
                if d in visited or s == d:
                    continue
                # 找距离最小的点
                if graph[s][d] < distance:
                    distance = graph[s][d]
                    # 将此边加入路径
                    pre = s
                    next = d
        path.append((pre, next))
        visited.append(next)
        nodes.remove(next)

    return path

def kruskal(graph):
    assert type(graph)==dict
    nodes = graph.keys()
    # 不同于prim，这里所有的进行排序
    visited = set()
    path = []
    next = None

    # 感觉这个效率比较低
    while len(visited) < len(nodes):
        distance = float('inf')
        # 找剩余没有通过边的最短路径
        for s in nodes:
            for d in nodes:
                # 边已经通过，继续
                if s in visited and d in visited or s == d:
                    continue
                if graph[s][d] < distance:
                    distance = graph[s][d]
                    pre = s
                    next = d
        # 将最小边加入节点
        path.append((pre, next))
        visited.add(pre)
        visited.add(next)

    return path

def dijkstra(graph, src):
    length = len(graph)
    type_ = type(graph)
    if type_ == list:
        nodes = [i for i in range(length)]
    elif type_ == dict:
        nodes = list(graph.keys())

    visited = [src]
    path = {src: {src: []}}
    nodes.remove(src)
    distance_graph = {src: 0}
    pre = next = src

    while nodes:
        distance = float('inf')
        for v in visited:
            for d in nodes:
                # 核心：起点到中间节点+中间节点到终点
                # 其中：中间节点为已访问节点，终点为未访问节点
                new_dist = graph[src][v] + graph[v][d]
                if new_dist <= distance:
                    distance = new_dist
                    next = d
                    pre = v
                    graph[src][d] = new_dist

        path[src][next] = [i for i in path[src][pre]]
        path[src][next].append(next)

        distance_graph[next] = distance

        visited.append(next)
        nodes.remove(next)

    return distance_graph, path

def floyd(graph):
    length = len(graph)
    path = {}
    for src in graph:
        path.setdefault(src, {})
        for dst in graph[src]:
            if src == dst:
                continue
            path[src].setdefault(dst, [src,dst])
            new_node = None

            for mid in graph:
                if mid == dst:
                    continue
                # 距离相加
                new_len = graph[src][mid] + graph[mid][dst]
                if graph[src][dst] > new_len:
                    graph[src][dst] = new_len
                    new_node = mid
            if new_node:
                path[src][dst].insert(-1, new_node)

    return graph, path


def getEdges(G):
    """ 读入图G，返回其边与端点的列表 """

    v1 = []  # 出发点
    v2 = []  # 对应的相邻到达点
    w = []  # 顶点v1到顶点v2的边的权值
    for i in G:
        for j in G[i]:
            if G[i][j] != 0:
                w.append(G[i][j])
                v1.append(i)
                v2.append(j)
    return v1, v2, w


def Bellman_Ford(G, v0, INF=999):
    v1, v2, w = getEdges(G)
    # 初始化源点与所有点之间的最短距离
    dis = dict((k, INF) for k in G.keys())
    dis[v0] = 0

    # 核心算法
    for k in range(len(G) - 1):  # 循环 n-1轮

        check = 0  # 用于标记本轮松弛中dis是否发生更新
        for i in range(len(w)):  # 对每条边进行一次松弛操作
            if dis[v1[i]] + w[i] < dis[v2[i]]:
                dis[v2[i]] = dis[v1[i]] + w[i]
                check = 1
        if check == 0: break

    # 检测负权回路
    # 如果在 n-1 次松弛之后，最短路径依然发生变化，则该图必然存在负权回路
    flag = 0
    for i in range(len(w)):  # 对每条边再尝试进行一次松弛操作
        if dis[v1[i]] + w[i] < dis[v2[i]]:
            flag = 1
            break
    if flag == 1:
        #         raise CycleError()
        return False
    return dis

if __name__ == '__main__':
    graph_dict = {"s1": {"s1": 0, "s2": 2, "s10": 3, "s12": 4, "s5": 3},
                  "s2": {"s1": 1, "s2": 0, "s10": 4, "s12": 2, "s5": 2},
                  "s10": {"s1": 2, "s2": 6, "s10": 0, "s12": 3, "s5": 4},
                  "s12": {"s1": 3, "s2": 5, "s10": 2, "s12": 0, "s5": 2},
                  "s5": {"s1": 3, "s2": 5, "s10": 2, "s12": 4, "s5": 0},
                  }

    path1 = prim(graph_dict, 's12')
    print(path1)
    path = kruskal(graph_dict)
    print (path)
    distance, path = dijkstra(graph_dict, 's1')
    print(distance, '\n', path)
    new_graph, path= floyd(graph_dict)
    print (new_graph, '\n', path)
    dis = Bellman_Ford(graph_dict, 's1')
    print(dis)
Donate comment here